One can measure the rain falling at a place by placing a measuring cylinder graduated in a length scale, commonly in mm. In this way, we are not measuring the volume of water that is stored in the cylinder, but the ‘depth’ of rainfall. The cylinder can be of any diameter, and we would expect the same ‘depth’ even for large diameter cylinders provided the rain that is falling is uniformly distributed in space.
Now think of a cylinder with a diameter as large as a town, or a district or a catchment of a river. Naturally, the rain falling on the entire area at any time would not be the same and what one would get would be an ‘average depth’. Hence, to record the spatial variation of rain falling over an area, it is better to record the rain at a point using a standard sized measuring cylinder.
In practice, rain is mostly measured with the standard non-recording rain gauge the details of which are given in Bureau of Indian Standards code IS 4989: 2002. The rainfall variation at a point with time is measured with a recording rain-gauge, the details of which may be found in IS 8389: 2003. Modern technology has helped to develop Radars, which measures rainfall over an entire region. However, this method is rather costly compared to the conventional recording and non-recording rain gauges which can be monitored easily with cheap labour.
Now think of a cylinder with a diameter as large as a town, or a district or a catchment of a river. Naturally, the rain falling on the entire area at any time would not be the same and what one would get would be an ‘average depth’. Hence, to record the spatial variation of rain falling over an area, it is better to record the rain at a point using a standard sized measuring cylinder.
In practice, rain is mostly measured with the standard non-recording rain gauge the details of which are given in Bureau of Indian Standards code IS 4989: 2002. The rainfall variation at a point with time is measured with a recording rain-gauge, the details of which may be found in IS 8389: 2003. Modern technology has helped to develop Radars, which measures rainfall over an entire region. However, this method is rather costly compared to the conventional recording and non-recording rain gauges which can be monitored easily with cheap labour.
Rainfall measurement is commonly used to estimate the amount of water falling over the land surface, part of which infiltrates into the soil and part of which flows down to a stream or river. For a scientific study of the hydrologic cycle, a correlation is sought, between the amount of water falling within a catchment, the portion of which that adds to the ground water and the part that appears as streamflow. Some of the water that has fallen would evaporate or be extracted from the ground by plants.
Average rainfall depth The time of rainfall record can vary and may typically range from 1 minute to 1 day for non – recording gauges, Recording gauges, on the other hand, continuously record the rainfall and may do so from 1 day 1 week, depending on the make of instrument. For any time duration, the average depth of rainfall falling over a catchment can be found by the following three methods.
• The Arithmetic Mean Method
• The Thiessen Polygon Method
• The Isohyetal Method
Arithmetic Mean Method
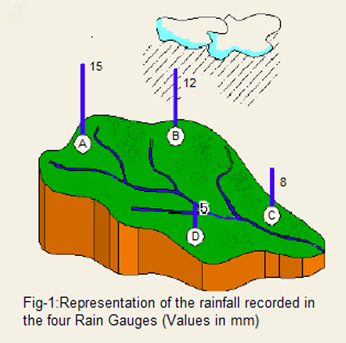
The simplest of all is the Arithmetic Mean Method, which taken an average of all the rainfall depths as shown in Figure 1.
The Theissen polygon method
This method, first proposed by Thiessen in 1911, considers the representative area for each rain gauge. These could also be thought of as the areas of influence of each rain gauge, as shown in Figure 2.
This method, first proposed by Thiessen in 1911, considers the representative area for each rain gauge. These could also be thought of as the areas of influence of each rain gauge, as shown in Figure 2.
These areas are found out using a method consisting of the following three steps:
1. Joining the rain gauge station locations by straight lines to form triangles
2. Bisecting the edges of the triangles to form the so-called “Thiessen polygons”
3. Calculate the area enclosed around each rain gauge station bounded by the polygon edges (and the catchment boundary, wherever appropriate) to find the area of influence corresponding to the rain gauge.
For the given example, the “weighted” average rainfall over the catchment is determined as,

1. Joining the rain gauge station locations by straight lines to form triangles
2. Bisecting the edges of the triangles to form the so-called “Thiessen polygons”
3. Calculate the area enclosed around each rain gauge station bounded by the polygon edges (and the catchment boundary, wherever appropriate) to find the area of influence corresponding to the rain gauge.
For the given example, the “weighted” average rainfall over the catchment is determined as,

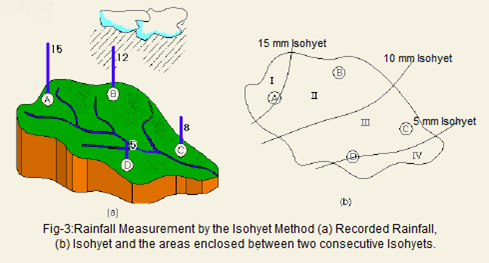
The Isohyetal method
This is considered as one of the most accurate methods, but it is dependent on the skill and experience of the analyst. The method requires the plotting of isohyets as shown in the figure and calculating the areas enclosed either between the isohyets or between an isohyet and the catchment boundary. The areas may be measured with a planimeter if the catchment map is drawn to a scale.
This is considered as one of the most accurate methods, but it is dependent on the skill and experience of the analyst. The method requires the plotting of isohyets as shown in the figure and calculating the areas enclosed either between the isohyets or between an isohyet and the catchment boundary. The areas may be measured with a planimeter if the catchment map is drawn to a scale.
For the problem shown in Figure 3, the following may be assumed to be the areas enclosed between two consecutive isohyets and are calculated as under:
Area I = 40 km2
Area II = 80 km2
Area III = 70 km2
Area IV = 50 km2
Total catchment area = 240 km2
The areas II and III fall between two isohyets each. Hence, these areas may be thought of as corresponding to the following rainfall depths:
Area II : Corresponds to (10 + 15)/2 = 12.5 mm rainfall depth
Area III : Corresponds to (5 + 10)/2 = 7.5 mm rainfall depth
For Area I, we would expect rainfall to be more than 15mm but since there is no record, a rainfall depth of 15mm is accepted. Similarly, for Area IV, a rainfall depth of 5mm has to be taken.
Hence, the average precipitation by the isohyetal method is calculated to be
Area I = 40 km2
Area II = 80 km2
Area III = 70 km2
Area IV = 50 km2
Total catchment area = 240 km2
The areas II and III fall between two isohyets each. Hence, these areas may be thought of as corresponding to the following rainfall depths:
Area II : Corresponds to (10 + 15)/2 = 12.5 mm rainfall depth
Area III : Corresponds to (5 + 10)/2 = 7.5 mm rainfall depth
For Area I, we would expect rainfall to be more than 15mm but since there is no record, a rainfall depth of 15mm is accepted. Similarly, for Area IV, a rainfall depth of 5mm has to be taken.
Hence, the average precipitation by the isohyetal method is calculated to be
Please note the following terms used in this section:
Isohyets: Lines drawn on a map passing through places having equal amount of rainfall recorded during the same period at these places (these lines are drawn after giving consideration to the topography of the region).
Planimeter: This is a drafting instrument used to measure the area of a graphically represented planar region.Isohyets: Lines drawn on a map passing through places having equal amount of rainfall recorded during the same period at these places (these lines are drawn after giving consideration to the topography of the region).
Mean rainfall
This is the average or representative rainfall at a place. The mean annual rainfall is determined by averaging the total rainfall of several consecutive years at a place. Since the annual rainfall varies at the station over the years, a record number of years are required to get a correct estimate.
Similarly, the mean monthly rainfall at a place is determined by averaging the monthly total rainfall for several consecutive years.
This is the average or representative rainfall at a place. The mean annual rainfall is determined by averaging the total rainfall of several consecutive years at a place. Since the annual rainfall varies at the station over the years, a record number of years are required to get a correct estimate.
Similarly, the mean monthly rainfall at a place is determined by averaging the monthly total rainfall for several consecutive years.